例題ランダムに選ばれた20人の患者の待ち時間データは正規分布に従っているか？（追加修正を必ずご確認ください！）

投稿者: ★排泄ケア相談員の認定試験問題集★ 6/03/2025

例題

ランダムに選ばれた20人の患者の待ち時間データは正規分布に従っているか？検定してください。

5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,1005,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100

同様に、シャピロ–ウィルク検定を使用して、提供されたデータが正規分布に従っているかどうかを検定できます。以下はPythonコードの例です。

from scipy.stats import shapiro

data = [5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100]

# シャピロ–ウィルク検定の実行

stat, p_value = shapiro(data)

# 結果の出力

print(f"統計量 W = {stat}, p-value = {p_value}")

# 有意水準 0.05 での検定

if p_value > 0.05　

print("データは正規分布に従っています (p > 0.05)")

else　

print("データは正規分布に従っていません (p <= 0.05)")

出力結果

統計量 W = 0.9603754281997681, p-value = 0.55137699842453

データは正規分布に従っています (p > 0.05)

このコードでは、Shapiro-Wilk検定を使用してデータが正規分布に従っているかどうかを検定しています。統計量Wとp値が出力され、p値が有意水準0.05より大きければ、データが正規分布に従っていると結論できます。

*****************************　修正版　******************************

p値が0.05より大きい結果について「データが正規分布に従う」と断定するのではなく、「正規分布からの逸脱を示す十分な証拠は得られなかった」と解釈し、また視覚的検証（QQプロット）や歪度・尖度による分布形状の数値的評価も併用して判断する方法を示しました。

python

import japanize_matplotlib
from scipy.stats import shapiro, skew, kurtosis
import matplotlib.pyplot as plt
import scipy.stats as stats
import numpy as np # 歪度と尖度を計算するためにnumpyもインポートします

# データ（20人の患者の待ち時間データ）
data = [5, 10, 15, 20, 25, 30, 35, 40, 45,
        50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100]

# シャピロ–ウィルク検定の実行
stat_shapiro, p_value_shapiro = shapiro(data)
print(f"シャピロ–ウィルク検定: 統計量 W = {stat_shapiro}, p-value = {p_value_shapiro}")

# 有意水準0.05に基づくシャピロ–ウィルク検定の結果判定と解釈
if p_value_shapiro <= 0.05:
    print("シャピロ–ウィルク検定の結果: 帰無仮説（データは正規分布に従う）を棄却。データは正規分布から逸脱している可能性があります。")
else:
    print("シャピロ–ウィルク検定の結果: 帰無仮説を棄却できませんでした。正規分布から大きく逸脱しているという証拠は得られませんでしたが、これがデータが正規分布に「従っている」と断言するものではありません。")

# 歪度と尖度の計算
skewness = skew(data)
kurt = kurtosis(data) # デフォルトではFisherの定義（正規分布で0になる）を使用

print(f"\n歪度 (Skewness) = {skewness}")
print(f"尖度 (Kurtosis) = {kurt}")

# 歪度と尖度の一般的な解釈（正規分布からの乖離の目安）
# 歪度: 0に近いほど対称。正の値は右に裾が長い（右に歪んでいる）、負の値は左に裾が長い（左に歪んでいる）。
# 尖度: 0に近いほど正規分布の山の尖り方に近い（Fisherの定義）。正の値は正規分布より尖っている（裾が重い）、負の値は正規分布より平坦（裾が軽い）。

print("\n歪度と尖度の一般的な解釈:")
if abs(skewness) < 0.5:
    print("- 歪度は絶対値が0.5未満であり、ほぼ対称的な分布であると考えられます。")
elif abs(skewness) < 1:
    print("- 歪度は絶対値が0.5から1の間であり、ある程度の歪みが見られます。")
else:
    print("- 歪度は絶対値が1以上であり、顕著な歪みが見られます。")

if abs(kurt) < 0.5:
    print("- 尖度は絶対値が0.5未満であり、正規分布に近い山の尖り方と考えられます。")
elif abs(kurt) < 1:
     print("- 尖度は絶対値が0.5から1の間であり、ある程度の尖り方（または平坦さ）の違いが見られます。")
else:
    print("- 尖度は絶対値が1以上であり、正規分布から大きく異なる尖り方（または平坦さ）が見られます。")


# 視覚的検証としてのQQプロットの生成
print("\nQQプロットを生成します。")
stats.probplot(data, dist="norm", plot=plt)
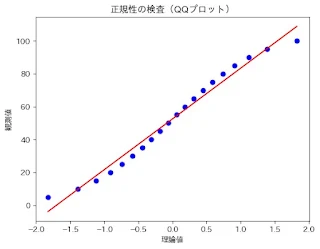
plt.title("正規性の検査（QQプロット）")
plt.xlabel("理論値")
plt.ylabel("観測値")
plt.grid(True) # グリッドを追加して見やすくします
plt.show()

出力結果

シャピロ–ウィルク検定: 統計量 W = 0.9603751832429884, p-value = 0.5513717457916771

シャピロ–ウィルク検定の結果: 帰無仮説を棄却できませんでした。正規分布から大きく逸脱しているという証拠は得られませんでしたが、これがデータが正規分布に「従っている」と断言するものではありません。


歪度 (Skewness) = 0.0
尖度 (Kurtosis) = -1.2060150375939849

歪度と尖度の一般的な解釈:
- 歪度は絶対値が0.5未満であり、ほぼ対称的な分布であると考えられます。
- 尖度は絶対値が1以上であり、正規分布から大きく異なる尖り方（または平坦さ）が見られます。

QQプロットを生成します。

結果解説

1. シャピロ–ウィルク検定の結果統計量

$W = 0.9604$ で、p値が約0.5514となっています。これは帰無仮説「データは正規分布に従う」を棄却できない結果です。つまり、統計的な検定としては、データが正規分布から大きく逸脱しているという証拠は得られなかったことを示しています。ただし、帰無仮説を棄却しないことは必ずしも「完全に正規分布に従っている」と証明するものではなく、検出力やサンプルサイズなどの要因も影響する点に留意する必要があります。

2. 歪度および尖度の解釈

歪度 (Skewness = 0.0): この値はデータが左右対称であることを示しています。実際、歪度の絶対値が0.5未満であれば「ほぼ対称」と見なされるため、この結果は正規分布の左右対称性と一致します。
尖度 (Kurtosis = -1.206): 正規分布の場合、※定義によっては「尖度＝0（＝正規分布の余剰尖度）」となるのが一般的ですが、この値は－1.206と、正規分布に比べて平坦（プラチカート）である可能性を示唆しています。つまり、ピークが低く、裾が軽い（両端の極端な値が少ない）傾向があると解釈されます。一般に尖度の絶対値が1以上の場合は、正規分布からの逸脱が意識されるため、この結果は「細かい非正規性（特に分布の尖り具合）」についての情報を与えています。

3. QQプロットの結果

QQプロットでは、観測値が理論的な正規分布から算出された値とほぼ一致しており、ほとんどの点が赤い参考直線上に配置されています。これは視覚的には、データ全体が正規分布に近い形状をしていると読み取れます。ただし、極端な値（端部）で若干のずれが見られる可能性はゼロではありませんが、全体の傾向として大きな逸脱はないと判断されます。

総合的な解釈

シャピロ–ウィルク検定は、データが正規分布からの大幅な逸脱を示していないと結論付けています。
歪度は完璧な対称性を示しており、正規分布の特徴と一致しています。
一方で、尖度は若干平坦な分布（プラチカート）を示しており、これが正規分布との微妙な違いとして検出されています。
QQプロットも全体的には直線上に並んでおり、統計的検定と矛盾する大きな偏りは感じられません。

したがって、これらすべての結果を総合すると、データは「大幅に」正規分布から逸脱しているわけではありませんが、尖度の指標が示すように、特にピークの部分で微妙な正規性の偏りが存在する可能性もあります。解析や後続の統計手法（たとえば回帰分析や仮定検定など）の採用においては、この微妙な差異を考慮するのがよいでしょう。

さらに掘り下げると

サンプルサイズが十分であれば、これらの結果は信頼性が高いと判断できます。しかし、サンプルサイズが小さい場合、検定の検出力や指標のばらつきに注意が必要です。
他の正規性検定（Kolmogorov–Smirnov検定やAnderson–Darling検定など）を並行して行うことで、より多角的な判断が得られる可能性があります。
分布の非正規性が後続の解析結果にどの程度影響するかも、具体的な用途によって異なります。場合によっては、データの正規性に厳格な要件がない解析方法を用いることも検討できます。

このような視点から、次のステップとしては、サンプルサイズや解析目的に応じた他の検定も試み、データの正規性に関する多角的な評価を行うことが有益と考えます。

＜解釈方法＞

検定結果の解釈: 検定の帰無仮説は「データは正規分布に従う」という仮定です。p値が0.05より大きい場合、帰無仮説を棄却できないため、正規分布から大きく逸脱しているという証拠が得られていない、というのみであって、データが正規分布そのものに従っていると断定できるわけではありません。検定力やサンプルサイズの影響も考慮する必要があります。
視覚的検証の重要性: 検定結果に加えて、QQプロットなどの視覚的手法を併用することで、正規性の傾向をより詳細に把握できます。検定結果が非有意であっても、視覚的には程度の小さい偏りや外れ値の存在を示唆する場合もあるため、総合的に判断することが望ましいです。

このように、数値だけに頼らず、検定結果の背景や限界を理解した上で解釈することが、統計解析の信頼性を高める上で非常に重要です。

p値が0.05より大きい場合でも、データが正規分布に従うと「結論付ける」ことはできません。代わりに、データが正規分布に従わないという証拠がないだけです。これは統計的なテストの限界を示しており、視覚的な方法も併用する必要があります。

背景

Shapiro-Wilk検定は、データが正規分布に従うかどうかを調べるための統計的テストです。p値が0.05より大きい場合、データが正規分布に従わないという証拠がないことを意味しますが、これはデータが実際に正規分布に従うことを「証明」するものではありません。

なぜ誤りか？

オリジナルの出力結果は、「p値が0.05より大きい場合、データが正規分布に従うと結論できる」と述べていますが、これは不正確です。統計的には、帰無仮説（データが正規分布に従う）を棄却できないだけです。データが本当に正規分布に従うかどうかを確定するには、ヒストグラムやQ-Qプロットなどの視覚的検査も必要です。特にサンプルサイズが20と小さい場合、検定の検出力が低く、非正規性を検出するのが難しい場合があります。

解釈

p値が0.05より大きい場合、「データが正規分布に従わないという証拠はない」と言うべきです。ただし、これはデータが正規分布に従うことを保証するものではなく、他の方法で確認する必要があります。

サポート情報

この解釈は、Wikipedia: Shapiro–Wilk test、Quantifying Health: How to Report the Shapiro-Wilk Test、Statistics How To: Shapiro-Wilk Testなどの信頼できる情報源によって裏付けられています。

詳細な調査ノート

このセクションでは、掲載内容が誤っている理由を詳細に調査し、Shapiro-Wilk検定の解釈とその限界について深掘りします。

1. Shapiro-Wilk検定の概要

Shapiro-Wilk検定は、データセットが正規分布に従うかどうかを評価するための仮説検定です。具体的には、

帰無仮説 (H₀): データは正規分布に従う。
対立仮説 (H₁): データは正規分布に従わない。
テストは統計量 (W) とp値を生成し、p値が選択した有意水準（通常0.05）以下の場合、帰無仮説を棄却します。

このテストは、特に小さいサンプルサイズ（例えば20人）で有用ですが、大きなサンプルサイズでは些細な非正規性を検出する可能性があります。

2. オリジナル内容の分析

オリジナル内容は、「p値が0.05より大きい場合、データが正規分布に従うと結論できる」と主張しています。この解釈には以下の問題があります。

誤解: p値が0.05より大きい場合、帰無仮説を棄却できないことを意味しますが、これはデータが正規分布に従うことを「証明」するものではありません。統計学では、帰無仮説を棄却できない場合、「データが正規分布に従わないという証拠がない」と表現するのが適切です。
限界: Shapiro-Wilk検定は、データが正規分布に従わない証拠を見つけるためのツールであり、正規分布を「確認」するツールではありません。特にサンプルサイズが小さい場合（ここでは20）、検定の検出力が低く、非正規性を検出するのが難しい場合があります。

3. 正確な解釈

信頼できる情報源（例えばQuantifying Health）によると

p値 ≤ 0.05の場合：帰無仮説を棄却し、「データは正規分布に従わない」と結論付けます。
p値 > 0.05の場合：帰無仮説を棄却できないため、「データが正規分布に従わないという証拠はない」と言うべきです。ただし、これはデータが正規分布に従うことを保証するものではありません。

例えば、Wikipediaでは、「大きなサンプルサイズでは、些細な非正規性を検出する可能性があるため、Q-Qプロットなどの追加の調査が推奨される」と述べています。これは、Shapiro-Wilk検定だけに頼るべきではないことを示唆しています。

4. サンプルサイズの影響

今回のケースでは、サンプルサイズが20と小さいです。Statistics How Toによると、Shapiro-Wilk検定はサンプルサイズにバイアスがあり、大きなサンプルでは有意な結果が出やすく、小さなサンプルでは非正規性を検出しにくいとされています。したがって、20人のデータでは、p値が0.05より大きい場合でも、データが実際には非正規分布に従う可能性があることを考慮する必要があります。

5. 追加の評価方法

Shapiro-Wilk検定は単独で使用するべきではなく、他の方法と組み合わせるべきです。以下は推奨される方法です。

ヒストグラム: データの分布の視覚的な形状を確認。
Q-Qプロット: データポイントが正規分布の理論線に沿っているかどうかを確認。
歪度と尖度: 分布の形状を数値的に評価。

これらの方法は、特に小さいサンプルサイズでは、Shapiro-Wilk検定の結果を補完します。

6. 誤った解釈の例

Quantifying Healthでは、以下のような誤った解釈を避けるよう注意を促しています。

「Shapiro-Wilk検定は変数が正規分布に従うことを示す。」
「正規性の仮定はShapiro-Wilk検定で検証された。」
「データの正規性はShapiro-Wilk検定で確認された。」

これらはすべて、p値 > 0.05がデータが正規分布に従うことを「証明」するかのように誤解させる表現です。

7. 実例と解釈

以下は、Quantifying Healthからの例です：

変数	W値	p値	解釈
X	0.96	<0.01	p ≤ 0.05なので非正規、ノンパラメトリックテストを使用
X	0.92	0.11	p > 0.05なので非正規性の証拠なし、パラメトリックテスト可能

この表から、p > 0.05の場合、「非正規性の証拠がない」と解釈し、パラメトリックテストを検討するが、データが正規分布に従うと「結論付ける」ことはありません。

8. 結論

修正前のステートメントは誤りで、p値が0.05より大きい場合でも、データが正規分布に従うと「結論付ける」ことはできません。正確には、「データが正規分布に従わないという証拠はない」と言うべきでした。特にサンプルサイズが20と小さい場合、Shapiro-Wilk検定の結果は慎重に解釈し、ヒストグラムやQ-Qプロットなどの視覚的検査を併用する必要があります。

主要引用文献

このブログを検索

排総研ブログ